揹帴婥妛嘦 墘廗栤戣3


栤1丂嬥懏媴偺億僥儞僔儍儖僄僱儖僊乕
丂(b)偼丄Q1傪曄悢偲傒偰暯曽姰惉偟偰嵟彫抣傪媮傔傑偡丅偙偙偵偼彂偄偰偁傝傑偣傫偑丄旝暘偟偰嬌抣傪媮傔傞曽朄偱傕夝偗傞傛偆偱偡丅


栤2 嬥懏墌摏傪棳傟傞揹棳偵傛傞帴応
丂傾儞儁乕儖偺朄懃傪梡偄偰夝偄偰偄偒傑偡丅
傑偢丄嬥懏墌摏偵偼岴偑奐偄偰偄側偄偲壖掕偟偰丄偦偺応崌偺撪奜偺帴懇枾搙傪寁嶼偟傑偡丅
師偵丄岴偺晹暘偺傒偵傛傞帴懇枾搙傪寁嶼偟丄偦偺寢壥傪堷偗偽摎偊偑摼傜傟傑偡丅
揹棳偑棳傟偰偄側偄岴偺晹暘傪偳偆張棟偡傞偐偑嵟戝偺億僀儞僩偱丄弶傔偵岴傪柍帇偟偰寁嶼偟丄岴偺晹暘偺寢壥傪堷偗偽夝偑摼傜傟傞偲偄偆偙偲傪抦偭偰偄側偄偲夝偗側偄栤戣偱偡丅

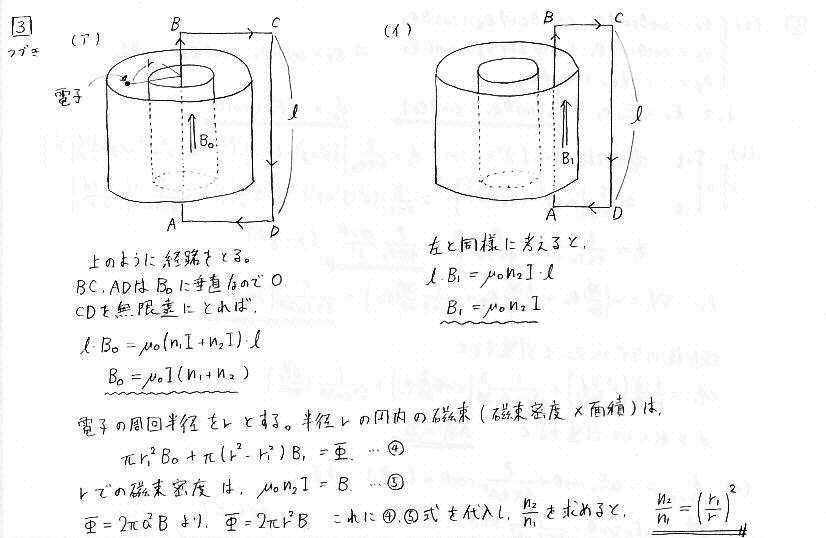
栤3 揹帴応偵傛傞揹巕偺壛懍
丂幉偑摨偠偱敿宎偑堎側傞僜儗僲僀僪偺娫偱揹巕傪壛懍偡傞忦審傪媮傔傑偡丅傾儞儁乕儖偺朄懃傪梡偄偰丄僜儗僲僀僪撪晹偱偺帴懇枾搙傪寁嶼偟傑偡丅

栤4 僜儗僲僀僪
丂帴懇枾搙偑帪娫偺娭悢偱昞傢偝傟傞偺偱丄揹帴桿摫偺朄懃偵戙擖偟偰寁嶼偟傑偡丅

栤5丂揹応拞偺摫懱媴
丂(a)偱偼丄z曽岦偺扨埵儀僋僩儖偑r丄兤丄冇曽岦偺扨埵儀僋僩儖偱偳偆昞傢偝傟傞偐傪寁嶼偟傑偡丅
(b)偱偼丄揹婥憃嬌巕偵傛傞億僥儞僔儍儖傪媴嵗昗昞帵偟偰寁嶼傪偟傑偡丅儔僾儔僔傾儞偼媴嵗昗偱偺宍傪巊偆昁梫偑偁傝傑偡丅
(c)偼丄昞柺偱惷揹億僥儞僔儍儖偑堦掕偲偄偆忦審傛傝丄r=a偵偍偗傞惷揹億僥儞僔儍儖偺兤旝暘偼僛儘偲偄偆偙偲傪梡偄傑偡丅
墘廗栤戣偺儁乕僕偵栠傞







