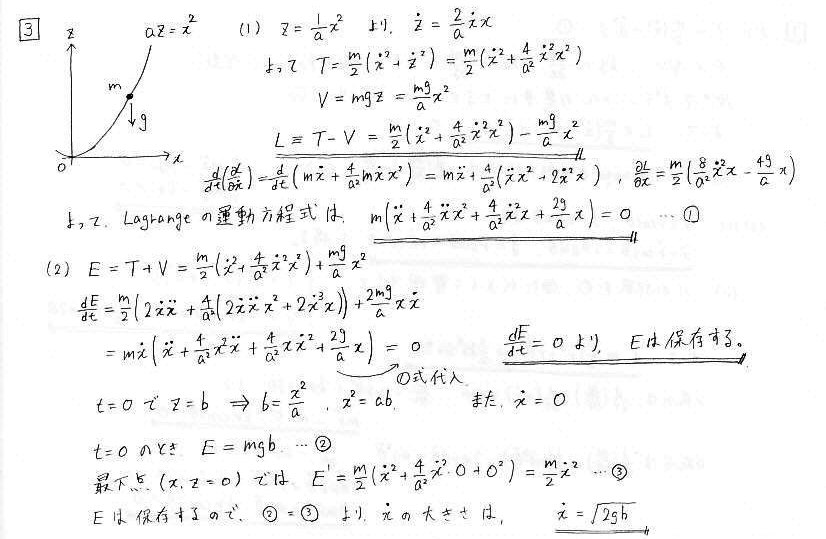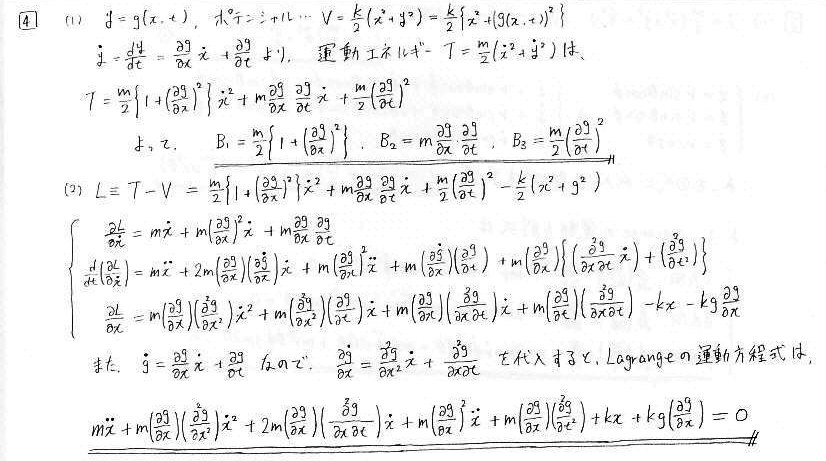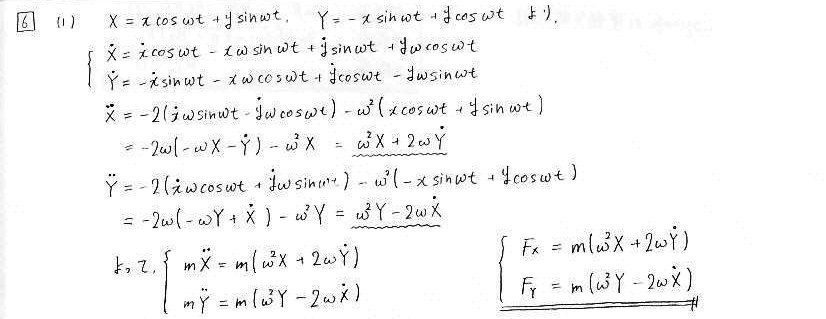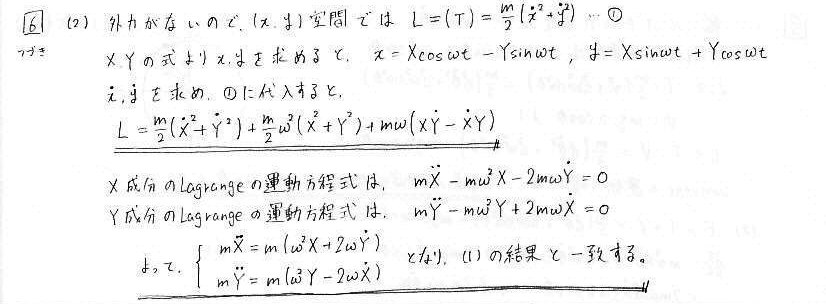解析力学Ⅰ 演習問題2

問1 Lagrangeの運動方程式
　(1)は、まず保存力からポテンシャルの形を求めます。そのあとラグランジアンを求め、Lagrangeの運動方程式を計算します。

問2 Lagrangeの運動方程式
　球座標でのラグランジアンを計算して、Lagrangeの運動方程式を計算します。

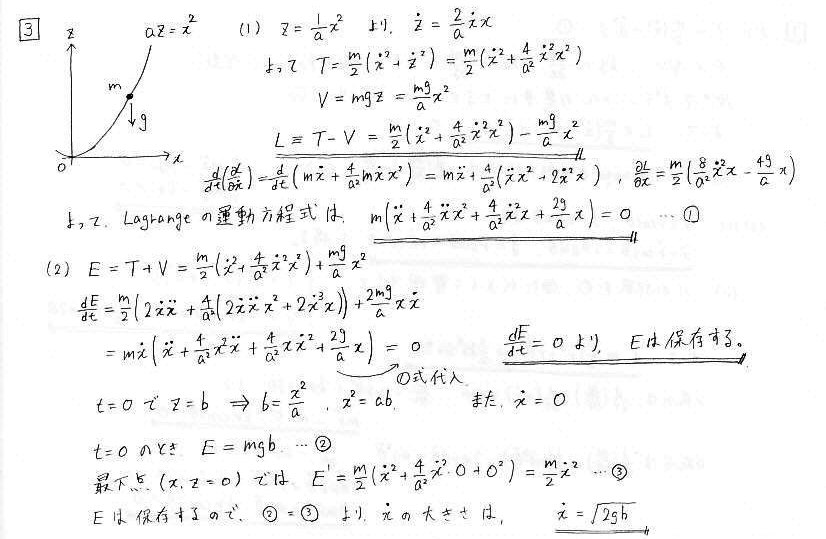
問3 拘束力のある場合のLagrangeの運動方程式
　zがxの関数で表わされるので、zを消去して考えます。

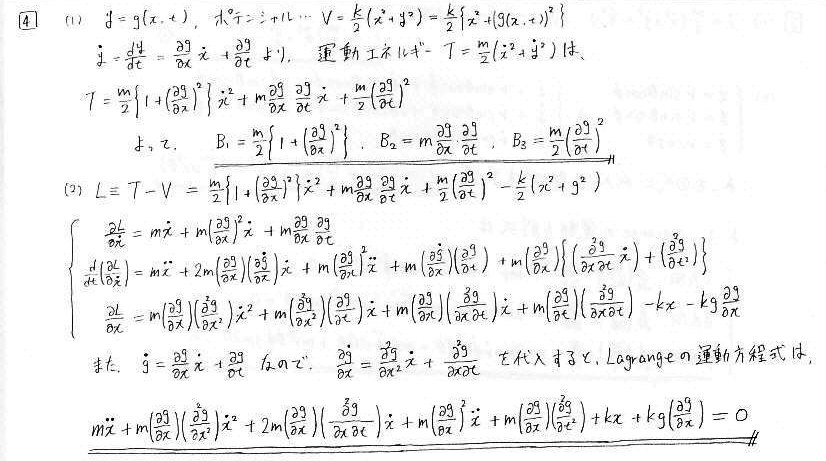
問4 拘束力のある場合のLagrangeの運動方程式
　yはxの関数で書けるということなので、yを消去します。yの具体的な形が与えられていないので計算が少々煩雑ですが、順番に計算していけば解が導けます。

問5 拘束力のある運動の解析
　条件より、変数はθのみとなるので、θに関する運動方程式を立てます。
(2)では、エネルギーは保存していませんが、dE/dtの式の形から、何らかの保存力があると考えます。その結果、エネルギーともう1つの項を合わせた量が保存していることが分かります。この項は遠心力ポテンシャルに相当します。

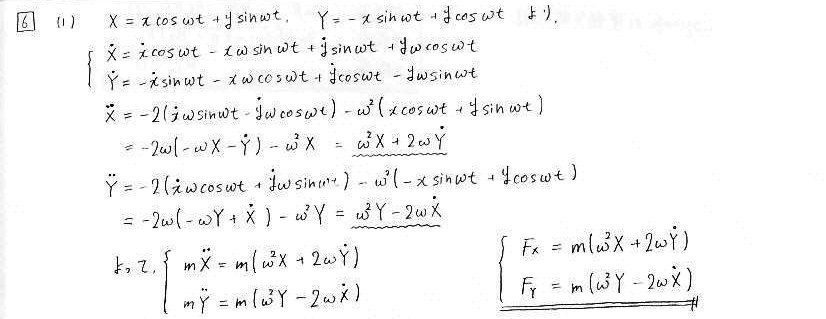
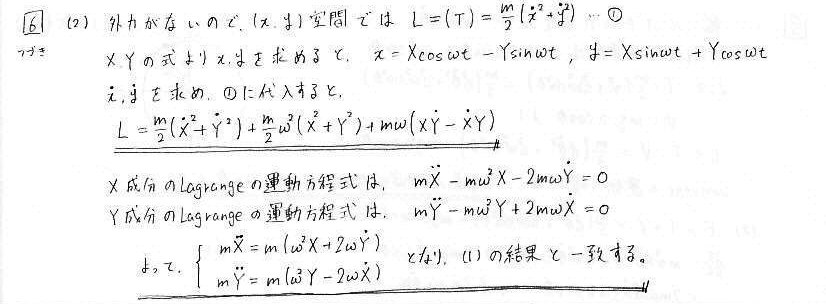
問6　回転座標
　変数変換の式が与えられているので、その式を使って計算していきます。

問7　電磁場中でのラグランジアン
　問題文の流れに沿って計算していけば解が導出できます。

演習問題のページに戻る