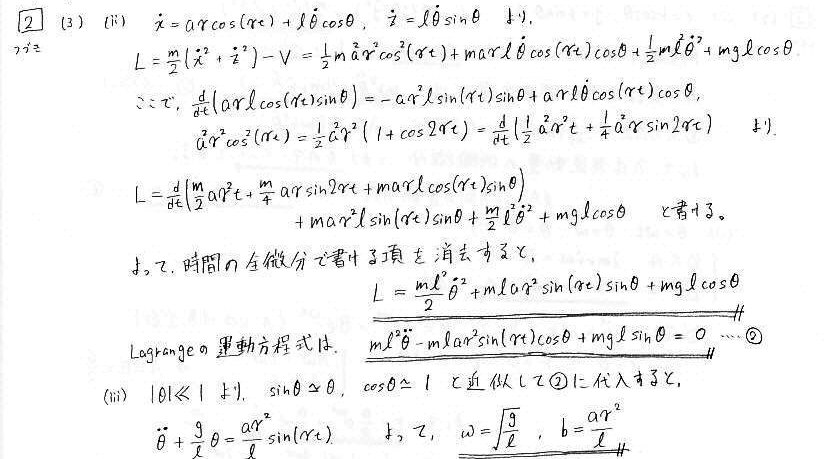解析力学Ⅰ 演習問題3

問1　変分原理
　問題文にあるδIの式から変分を求めます。部分積分の計算では、積分の範囲の両端では径路の変位は0なのでそれを利用して計算します。 (2)、(3)は具体的なラグランジアンが与えられている場合の計算です。

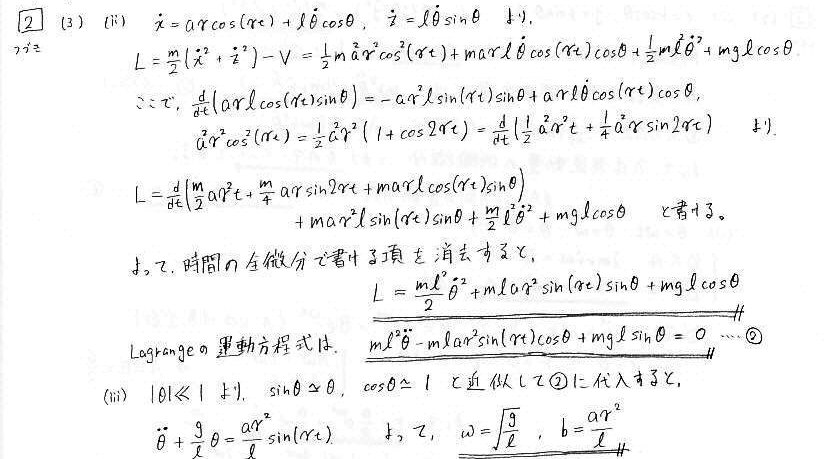
問2 Hamiltonの原理
　(1)では、変分が等しければ同じ運動方程式を導くことができることを示します。
(2)、(3)では、ラグランジアンを導出し、時間の全微分で書ける項は消去しても結果に差し支えないことを利用します。

問3 Lagrangeの未定乗数法
　拘束条件から、Lagkangeの未定乗数を導入して計算します。拘束条件の変分をとったとき、各座標の微小変化の係数部分がが未定乗数の係数となります。
(2)(ⅰ)では、λの式を変形して、λは角運動量の時間微分になることを示します。角運動量の微分は力のモーメントなので、この問題でのλは力のモーメントに相当します。

演習問題のページに戻る