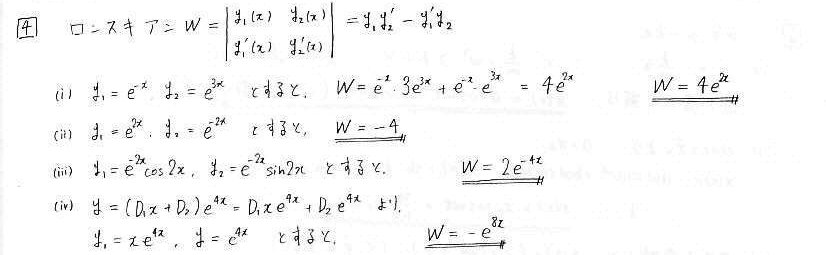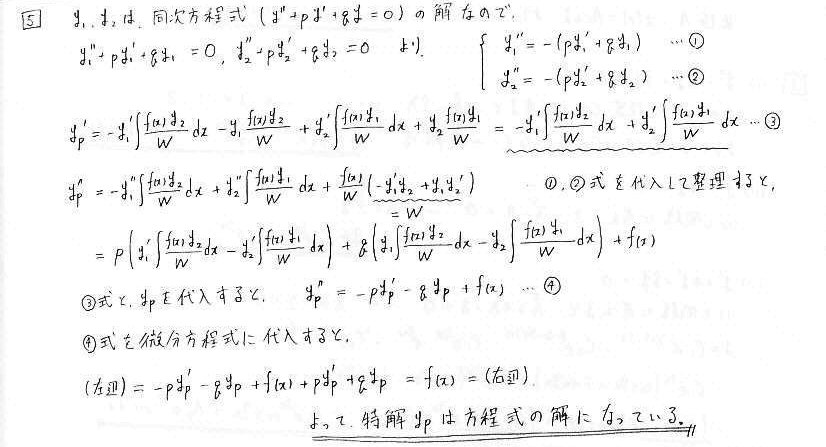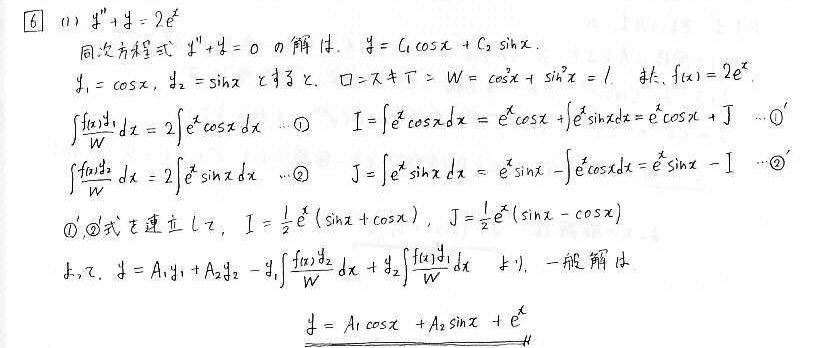悢棟暔棟妛嘥 墘廗栤戣2

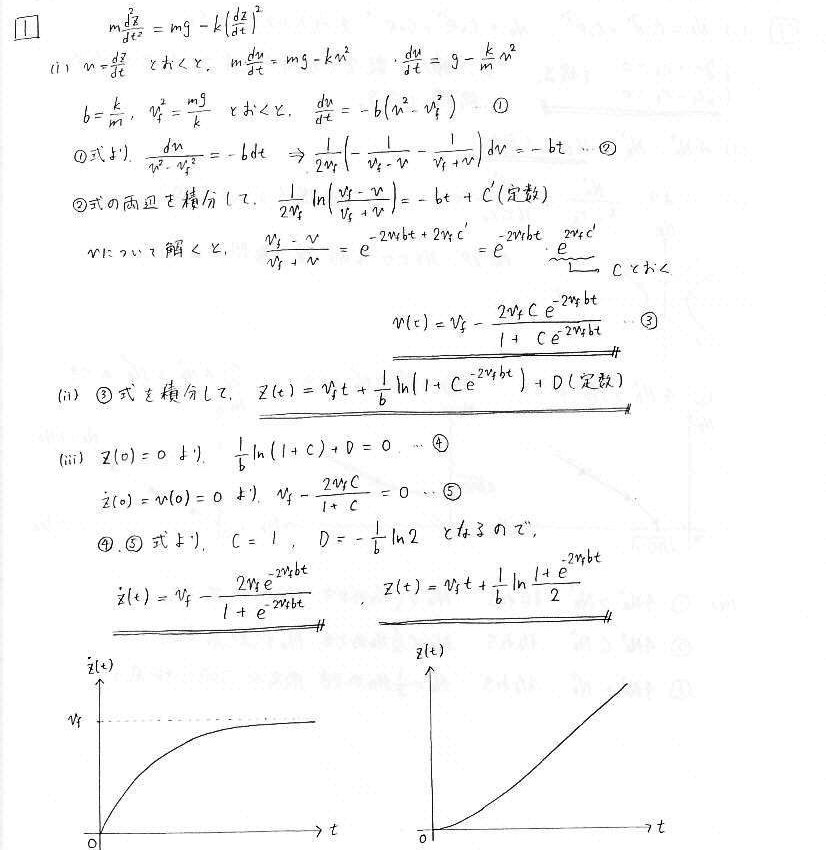
栤1 掞峈偺偁傞棊壓
丂栤戣偱梌偊傜傟偰偄傞捠傝偵曄悢傪v偵曄姺偟偰丄v偵懳偡傞堦斒夝傪媮傔傑偡丅曄悢暘棧傪偟偨嵺偵嘇幃偺傛偆側彮偟曄懃揑側幃曄宍傪偟傑偡丅
(鶥)偱偼丄梌偊傜傟偨弶婜忦審傪戙擖偟偰嬶懱揑側夝傪媮傔傑偡丅懍搙偺僌儔僼偼丄幃傪尒傞偲帪崗t偑戝偒偔側傞偵偮傟偰巜悢娭悢晹暘偑
僛儘偵廂懇偡傞偺偱丄掕悢vf偵嬤偯偒傑偡丅
z偺僌儔僼偼丄帪娫宱夁偲偲傕偵巜悢娭悢晹暘偑僛儘偵廂懇偟丄t偵娭偡傞1師娭悢晹暘偑巆傞偺偱丄t=0廃曈偱偼巜悢娭悢揑丄t>>1偱偼1師娭悢揑側
忋徃偵側傝傑偡丅

栤2 扨怳摦偺塣摦曽掱幃丂
丂(k/m)傪冎2偲抲偒偐偊傞偺偼屻偺曋媂偺偨傔偱丄帪偵寛傑傝偼偁傝傑偣傫丅夝傪媮傔偨偁偲丄夝偺宍偐傜偙偺宯偼
妏怳摦悢偑(k/m)偺暯曽崻偱昞傢偝傟傞偙偲偑暘偐傝傑偡丅
(鶥)偼丄弶婜忦審偵sin偺宍偑擖偭偰偄傞偺偱丄摼傜傟偨堦斒夝傪曄宍偟偰偐傜弶婜忦審傪戙擖偟傑偡丅

栤3 旝暘曽掱幃
丂栤戣暥偵偁傞傛偆偵夝傪壖掕偟偰戙擖偟丄摼傜傟偨兩偵娭偡傞曽掱幃(摿惈曽掱幃)傪夝偄偰堦斒夝傪媮傔傑偡丅
(鶥)偼摿惈曽掱幃偺夝偑暋慺悢偵側傝傑偡丅偦偺傑傑e偺尐偵忔偣偰偍偄偰傕栤戣側偄偱偡偑丄嶰妏娭悢偵捈偟偰偍偄偨傎偆偑夝偑偒傟偄側宍偵側傝傑偡丅
(鶦)偼丄摿惈曽掱幃偺夝偑廳夝偲側傝丄堦斒夝偑媮傔傜傟傑偣傫丅偦偺偨傔丄掕悢C傪x偺娭悢偲傒偰C(x)偲抲偒姺偊偰曽掱幃偵戙擖偡傞
乽掕悢曄壔朄乿傪梡偄傑偡丅
側偍丄摿惈曽掱幃偺夝偑兩=4偲側偭偰偄傞偨傔丄嵞傃曽掱幃偵戙擖偡傞嵺偼C(x)e4x偺宍偱戙擖偟偰偍偒傑偡丅
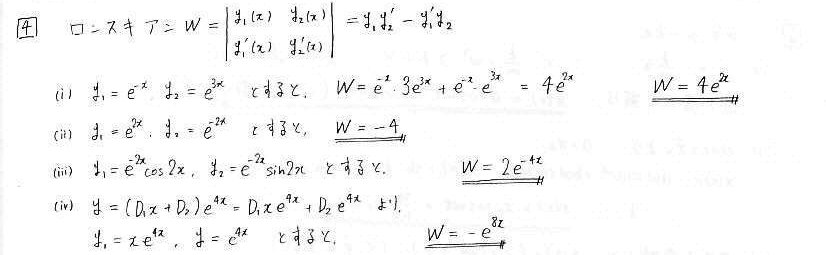
栤4 儘儞僗僉傾儞
丂栤3偱媮傔偨堦斒夝偼丄擇偮偺摿夝傪廳偹崌傢偣偨宍傪偟偰偄傑偡丅偦偺摿夝偐傜丄儘儞僗僉傾儞傪寁嶼偟傑偡丅
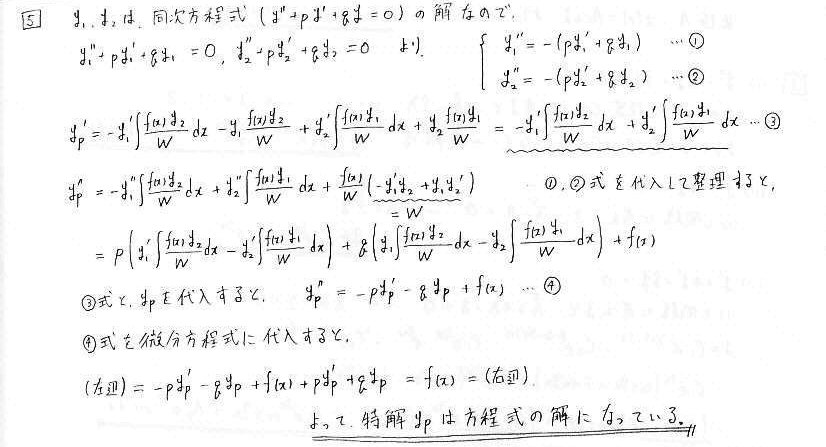
栤5 儘儞僗僉傾儞偲堦斒夝
丂栤戣暥偵偁傞幃偼丄慄宍旕摨師曽掱幃偺夝偺岞幃偺傛偆側傕偺偱偡丅偙傟偑杮摉偵夝偵側偭偰偄傞偐偳偆偐傪戙擖偟偰妋擣偟傑偡丅
y1丄y2偼"摨師曽掱幃偺夝"偱偁傞偙偲偵拲堄偟傑偡丅
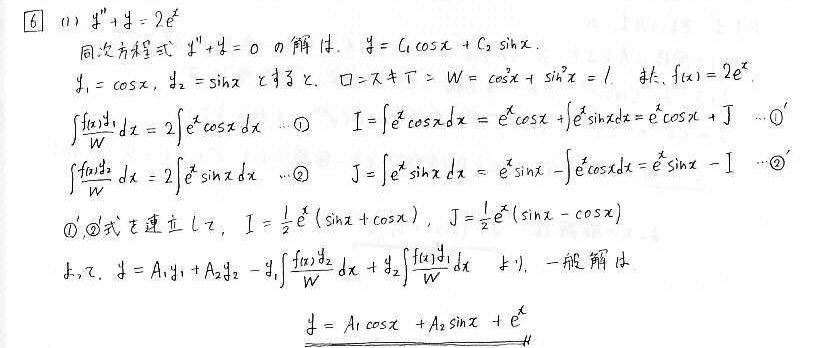

栤6 儘儞僗僉傾儞偲堦斒夝
丂栤5偺慄宍旕摨師曽掱幃偺夝偺岞幃傪梡偄偰丄梌偊傜傟偨曽掱幃偺堦斒夝傪媮傔傑偡丅
(鶣)偼愊暘偺寁嶼偵僥僋僯僢僋偑昁梫偱偡丅偍偦傜偔戝妛庴尡懳嶔偵偼傛偔偁傞丄擇偮偺幃傪楢棫偡傞曽朄偱寁嶼偟傑偡丅

栤7 怳傝巕偺塣摦
丂梙傟曽偺彫偝偄怳傝巕(兤偑彫偝偄)偱偼tan兤佮sin兤佮兤偺嬤帡偑巊偊傑偡偑丄偙偺応崌偼兤偼彫偝偄偲偼尷傜側偄偲偁傞偺偱
偦偺嬤帡偼巊偊傑偣傫丅
傑偨丄僌儔僼偼恾偺傛偆偵側傝丄兤=僛儘偱妏懍搙(兤偺帪娫旝暘)偑嵟戝偵側傝丄怳傝巕偺懍搙傕嵟戝偵側傝傑偡丅
偨偩偟丄弶懍搙偺戝偒偝偵傛傝丄兤亜(兾/2)偱偙偺恾偑惉傝棫偨側偔側傞偙偲偑峫偊傜傟傑偡丅
墘廗栤戣偺儁乕僕偵栠傞