悢棟暔棟妛嘥 墘廗栤戣3

栤1 尭悐怳摦偺旝暘曽掱幃
丂堦斒夝偼偄偮傕偺傛偆偵夝傪壖掕偟偰戙擖偟傑偡丅兞偺戝偒偝偵傛偭偰夝偑曄傢偭偰偔傞偺偱丄偦傟偧傟応崌暘偗偟傑偡丅
(鶥)偱偼丄梌偊傜傟偨悢抣偑偦傟偧傟偺応崌暘偗偺忦審偵懳墳偟偰偄傞偺偱丄応崌暘偗偵偁偭偨幃傊戙擖偟傑偡丅
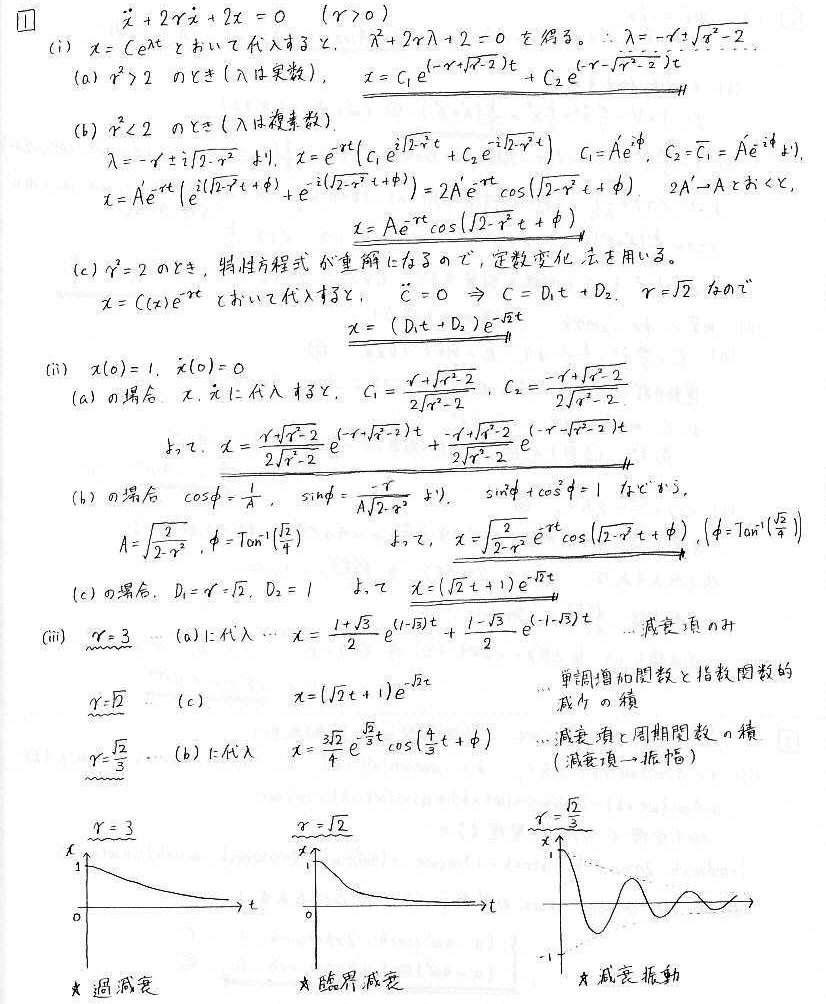
兞=併3偱偼巜悢娭悢夝偱丄偳偪傜傕尭彮偡傞夝側偺偱怳摦偼偣偢丄巜悢娭悢揑偵尭彮偟偰偄偒傑偡丅偙偺忬懺傪乽夁尭悐乿偲尵偄傑偡丅
兞=併2偱偼扨挷憹壛娭悢偲巜悢娭悢揑尭彮偺幃偺愊偵側偭偰偄傑偡偑丄巜悢娭悢偼媫懍偵0偵廂懇偡傞(巜悢娭悢偼傋偒娭悢傛傝嫮偄丄偲偄偆昞尰傪傛偔偡傞)偺偱0偵廂懇偡傞僌儔僼偵側傝傑偡丅
偙偺忬懺傪乽椪奅尭悐乿偲尵偄傑偡丅
嵟屻偺1偮偼丄巜悢娭悢揑尭彮偺崁偲cos偺愊偵側偭偰偄傞偺偱丄cos偵偐偐偭偰偄傞晹暘傪怳暆偲峫偊傞偲丄怳暆偑巜悢娭悢揑尭彮傪偡傞cos娭悢偲夝庍偱偒丄僌儔僼偼怳摦偟側偑傜0偵廂懇偟傑偡丅
偙偺忬懺偼乽尭悐怳摦乿偲偄偄丄杸嶤偺偁傞偽偹偺塣摦側偳偵懳墳偟偰偄傑偡丅
梋択偱偡偑丄墘廗扴摉偺愭惗偼乽亀椪奅尭悐亁偲偄偆尵梩偼偁傑傝椙偔側偄栿岅偱丄塣摦偺杮幙傪昞傢偟偰偄側偄乿偲尵偭偰偄傑偟偨丅

栤2 扨怳摦偺僄僱儖僊乕丂
丂(鶣)偺(a)(b)偼娙扨側寁嶼栤戣偱偡丅(c)偼幃傪巊偭偰寁嶼偟偰媮傔傑偡丅儮偼1廃婜偲偄偆偙偲傪棙梡偡傟偽丄sin丄cos偺愊暘偼0偵側傞偙偲偑暘偐傝傑偡丅
(2)(a)偼丄僄僱儖僊乕偺帪娫旝暘偲塣摦曽掱幃偺宍偐傜寁嶼偟傑偡丅

栤3 嫮惂怳摦
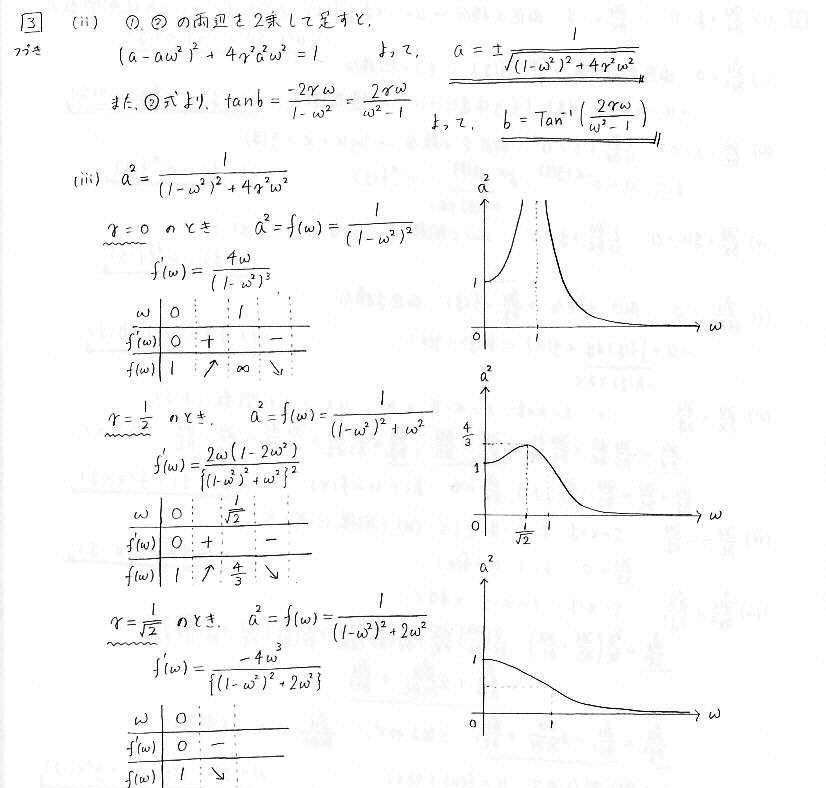
丂栤戣暥偱梌偊傜傟偰偄傞夝偺宍傪戙擖偟偰學悢傪寛掕偟傑偡丅
怳暆偺2忔偼丄兞偺抣偵傛偭偰怳傞晳偄偑曄傢偭偰偒傑偡丅怳暆傪冎偺娭悢偲傒偰丄偦傟偧傟偺応崌偺僌儔僼傪彂偒傑偡丅
墘廗栤戣偺儁乕僕偵栠傞




