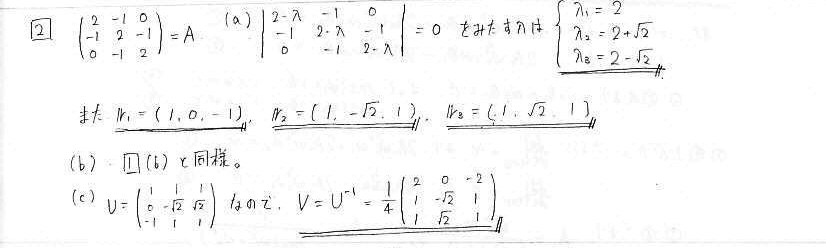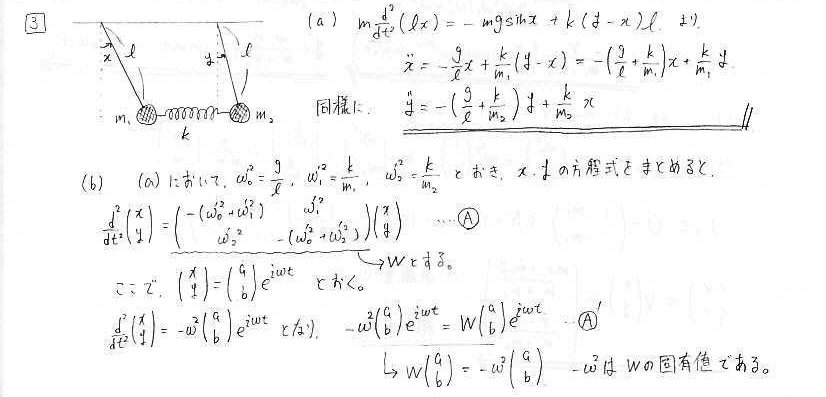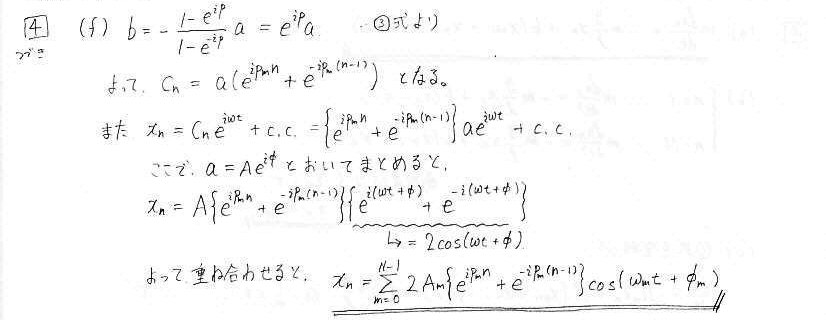悢棟暔棟妛嘦 墘廗栤戣2



栤1丂屌桳抣丒屌桳儀僋僩儖
丂扨弮側慄宍戙悢妛偺栤戣偱偡丅
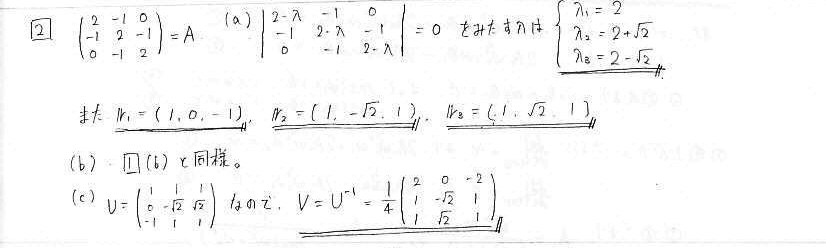
栤2 屌桳抣丒屌桳儀僋僩儖
丂栤1偺3亊3峴楍僶乕僕儑儞偱丄婎杮揑側寁嶼偼摨偠偱偡丅
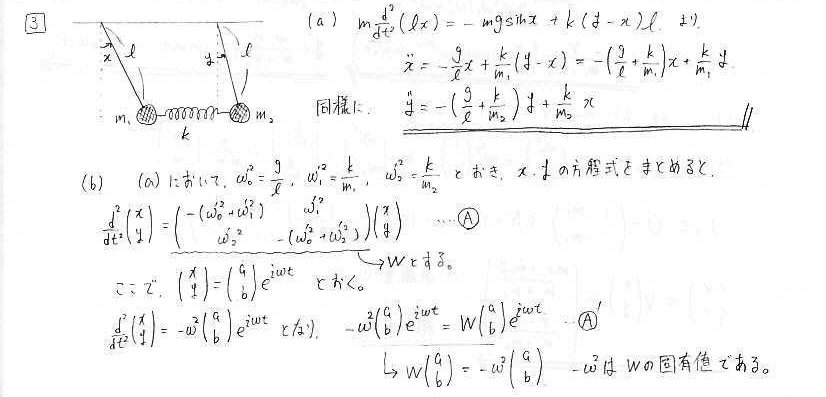

栤3 偽偹偱宷偑偭偨怳傝巕
丂(a)偺塣摦曽掱幃傪棫偰傞嵺丄杮棃偼曄埵偼lsinx偲彂偒傑偡偑丄x<<1偱偁傟偽sinx佮x偲嬤帡偱偒傞偺偱丄偦傟傪梡偄偰彂偄偰偄偒傑偡丅
婎弨嵗昗傪媮傔傞偲偒偼丄栤1偱偺(c)偺峫偊傪棙梡偟傑偡丅

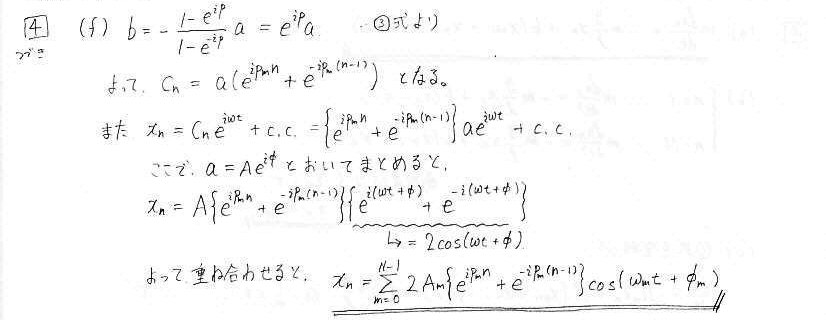
栤4 捈慄忋偺N屄偺怳傝巕偺夝愅
丂怳傝巕偺屄悢偑N屄偁傝傑偡偑丄偲傝偁偊偢1屄偺怳傝巕偺塣摦偵拝栚偟傑偡丅偙偺宯偺拞偱偺椺奜偼丄1斣栚偲N斣栚偺怳傝巕偱丄偙偺2偮偩偗曅曽偟偐宷偑偭偰偄傑偣傫丅
偙偺応崌偼丄0斣栚丄N亄1斣栚傪壖掕偟偰傗傞偙偲偱懠偺怳傝巕偲摨偠幃偱埖偆偙偲偑偱偒傑偡丅
(c)偱偼丄夝傪怳摦夝偱壖掕偟偰戙擖偟丄嵎暘曽掱幃(慟壔幃)傪媮傔傑偡丅
(d)偺丄怳摦悢偲攇悢偺娭學偺偙偲傪暘嶶娭學偲傛傃傑偡丅攇摦傪埖偆暘栰偱偼昿弌偺梡岅偱偡丅
堦斒夝傪媮傔傞偲偙傠偱偼丄1偮偵懳偡傞堦斒夝傪媮傔偨偁偲丄慡屄悢暘廳偹崌傢偣偰傗傟偽慡懱偺堦斒夝偵側傝傑偡丅

栤5丂墌娐忬偺N屄偺怳傝巕偺夝愅
丂夝偒巒傔偼栤4偲摨偠偱偡丅偨偩偟墌娐忬偵宷偑偭偰偄傞偺偱丄栤4偱壖掕偟偨0斣栚偺怳傝巕偼N斣栚偺怳傝巕丄N亄1斣栚偺怳傝巕偼1斣栚偺怳傝巕偵憡摉偟傑偡丅
偙偺傛偆側忦審傪乽廃婜揑嫬奅忦審乿(periodic boundary condition)偲尵偄傑偡丅
戝懱偺寁嶼偼栤4偲摨偠傛偆偵恑傔偰偄偒傑偡丅堦斒夝偼cos娭悢偱彂偗傑偡丅
墘廗栤戣偺儁乕僕偵栠傞