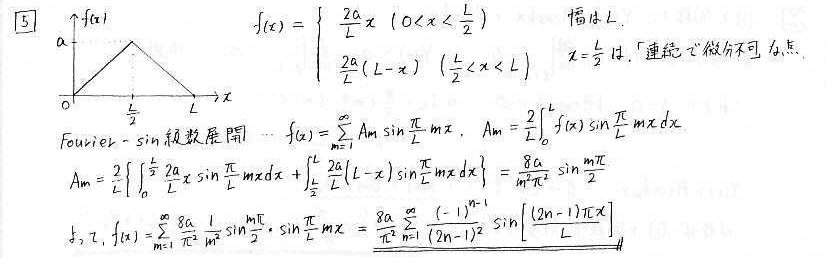数理物理学Ⅱ 演習問題3


問1 波動方程式
まずは1個の球について運動方程式を立てます。この式を変形していき、球の間隔を0にする極限をとれば波動方程式が導出できます。

問2 フーリエ級数展開
区間[0,L]なので、幅はLになります。
フーリエ級数展開とは、平たく言えば、おおよその関数は波動関数の重ね合わせで表現することができる、というものです。
sin関数で展開するか、cos関数で展開するか、あるいは両方で展開するなどの方法があります。方法によって式の定義が微妙に変わってくるので気をつけて計算していきます。
(b)のcosで展開する場合は、m=0のときだけ式の形が違うことに注意します。
式の概形はあまり元の関数と一致しているように見えませんが、重ね合わせを続けていくとだんだん近い形になっていきます。
(上では、n=1,2,3のそれぞれの形を書いています)
不連続点などでは一致しない部分もありますが、全体的に見て一致するという状況を、数学用語で「ほとんど至るところ(almost everywhere)で一致」と言います。
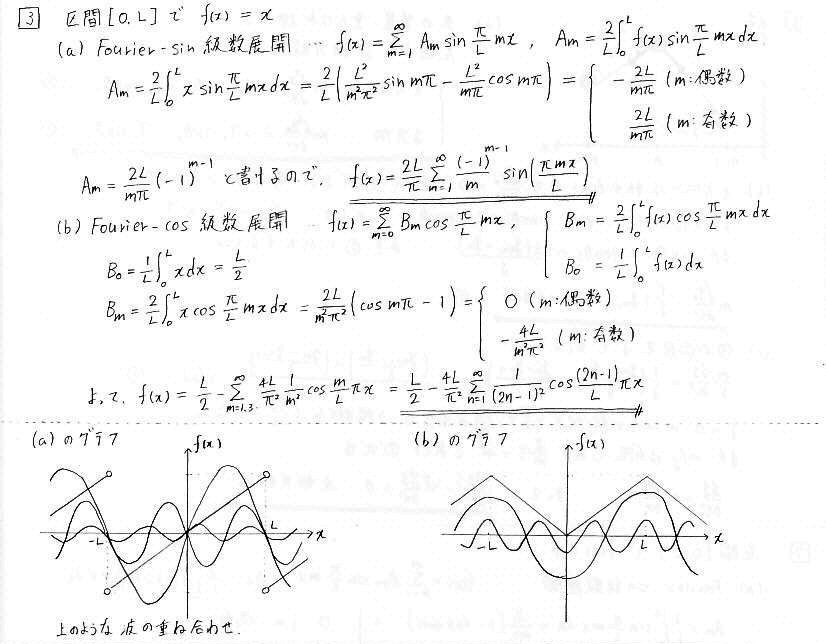
問3 フーリエ級数展開
計算の方法は問2とまったく同じです。

問4 フーリエ級数展開
ここでの展開はsin、cosの両方を用いた展開です。sinのみ、cosのみの展開の場合とは式の係数などが少しずつ違うことに注意して計算します。
Fourier級数展開は、展開する関数に不連続点があっても展開することができ、そこでの値は元の関数の右極限と左極限の間の値になっています。
ただし、不連続点の個数が無限個あるなど、展開できない条件も存在しますが、一般的な関数はほとんどが展開可能です。
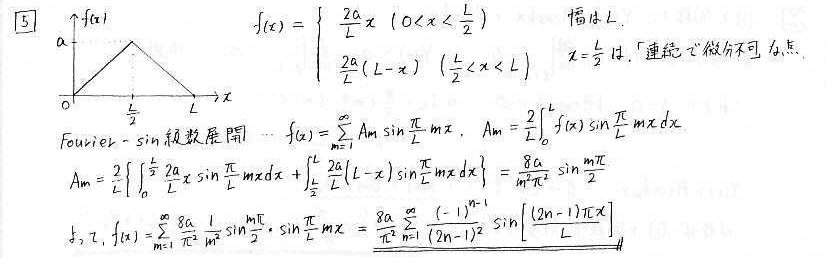
問5 フーリエ級数展開
今までの問題と解き方は一緒です。
演習問題のページに戻る