数理物理学Ⅱ 演習問題4

問1　波動方程式
　問題分に解を仮定してあるのでそれをそのまま代入します。c.cとは複素共役という意味の英語の略語です。

問2 波動方程式
　問1とは境界条件が違うので、解の形も変わってきます。計算の流れは同じです。

問3 フーリエ級数展開
　関数を展開する条件として、正規直交性を満たしているかというのが条件になってきます。正規直交性というのはベクトルでいう単位ベクトルのようなもので、確認の方法としては、添え字を変えた関数(上ではn、mで区別)をかけて展開する範囲で積分してやります。 (a)でまずその計算をしてやると、係数×(クロネッカーのデルタ)の形になるので、直交性は確認できました。そこで、「単位ベクトル」と同様に大きさが1であれば正規直交性が満たされます。そのため、sinの係数にπの平方根分の1を付け加えてやると、先ほどの積分結果は1になります。
(b)では、e^inxの形をした関数も正規直交性を満たすことを確認します。ここで注意するのは、積分するときには関数とその複素共役(かつ添え字を変えたもの)をかけるということです。そもそもの規格化(大きさを1にする)の条件が、(関数)×(関数の複素共役)の積分＝1　です。 cosがそのままなのは、cos関数は実数関数なので複素共役が同じだからです。

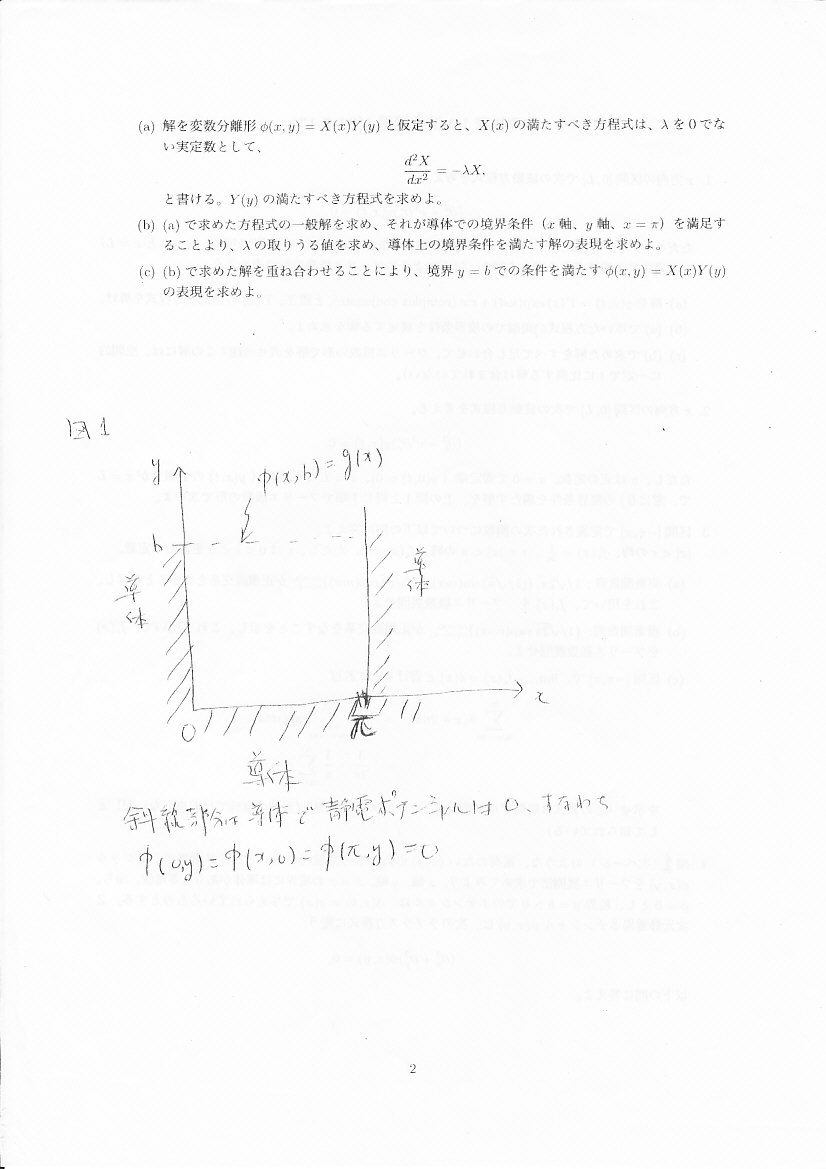
問4 2次元の波動方程式
　問題文に解の形が与えられているのでそれを代入し、XとYに分離します。
(b)は、一般的な微分方程式の問題なので、解いてから境界条件を用いて係数を決定していきます。一般解にn依存性があるのですべて足し合わせたものが解になります。
(c)は難しい問題ですが、境界条件を代入した式がFourier級数展開の形になっていることを利用して計算します。

演習問題のページに戻る