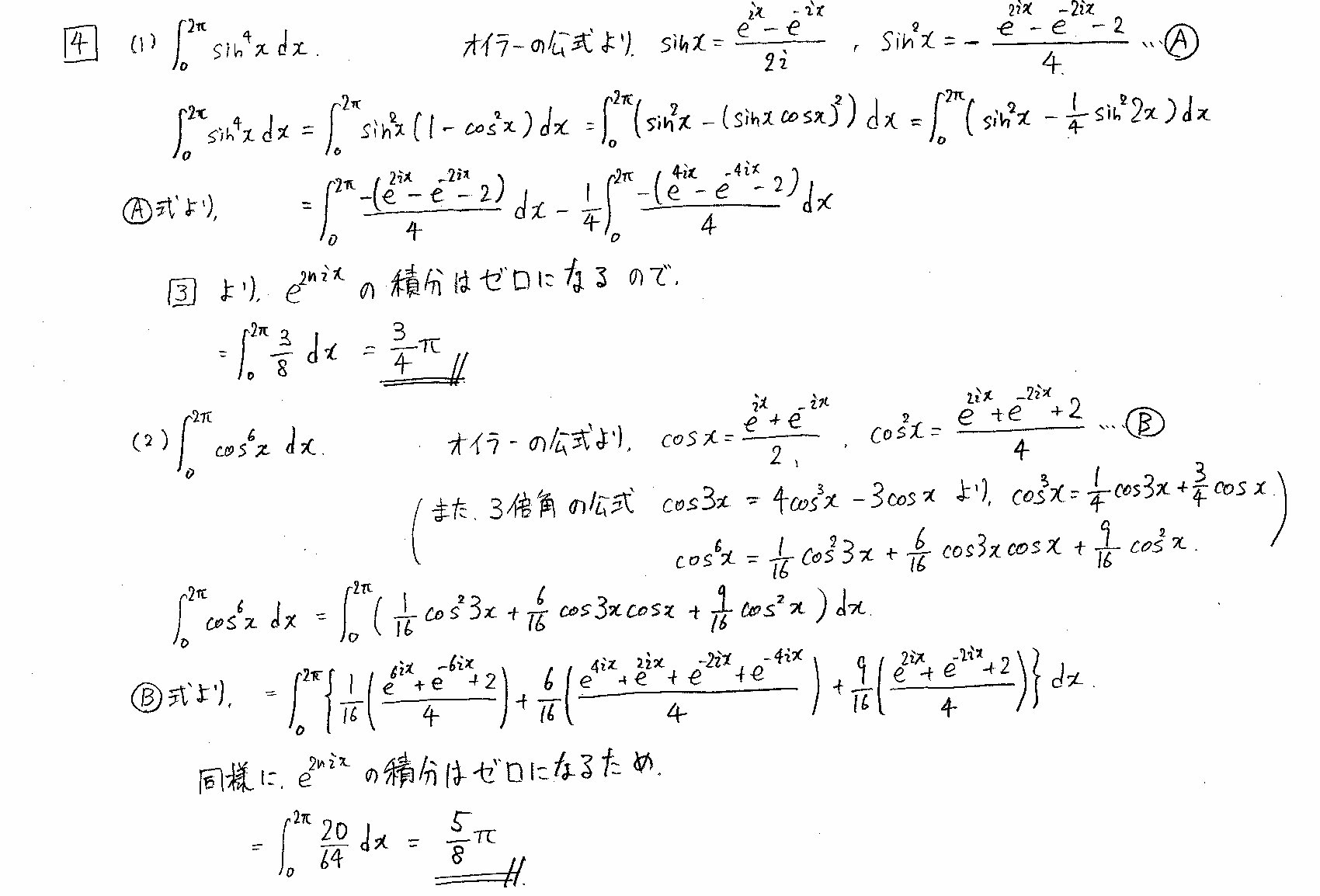悢棟暔棟妛嘦 墘廗栤戣1

PDF斉夝摎

栤1丂1偺n忔崻
丂丂n忔偡傞偲1偵側傞悢(暋慺悢)傪丄嬌昞帵偱昞偟偰偐傜r偲兤傪媮傔傑偡丅偡傋偰偺榓傪媮傔傞帪偼丄媺悢偺榓偺幃偐傜寁嶼偟傑偡丅尩枾側寁嶼偼暋慺娭悢榑偱廗偆偼偢乧丅偪側傒偵1偺n忔崻傪暋慺暯柺忋偵僾儘僢僩偟偰偄偔偲惓n妏宍偺捀揰偑昤偗傑偡丅

栤2丂僆僀儔乕偺岞幃
丂丂A偲B傪暿乆偵媮傔傞偺偼傎傏晄壜擻側偺偱丄cos偲sin偺宍偵側偭偰偄傞偙偲偵拲栚偟偰丄A亄iB傪摨帪偵寁嶼偟傑偡丅寁嶼寢壥偺幚晹偑A偺抣丄嫊晹偑B偺抣偵側傝傑偡丅

栤3丂僆僀儔乕偺岞幃
丂丂n=0偺応崌偺傒椺奜側偺偱婥傪偮偗偰寁嶼偟傑偡丅嵟屻偵僋儘僱僢僇乕偺僨儖僞偱夝傪彂偄偰偁傝傑偡偑丄偙偺婰崋傪巊偆偲僔儞僾儖偲偄偆偩偗偺榖偱偡丅(偨偩偟巊偄姷傟偰偍偔偲曋棙偱偡丅)
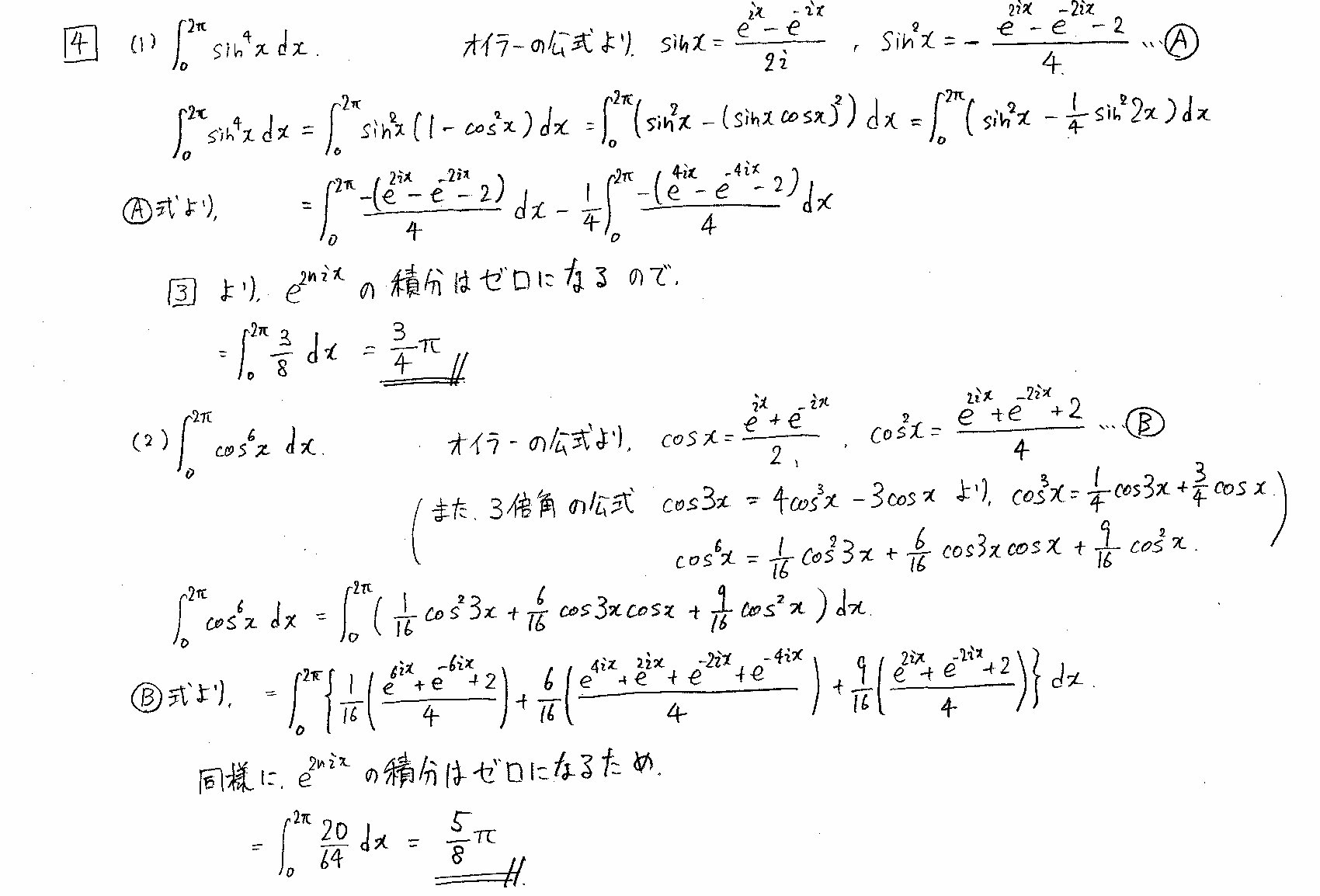
栤4丂僆僀儔乕偺岞幃
丂丂栤3偱媮傔偨愊暘寁嶼偺寢壥傪棙梡偟傑偡丅僆僀儔乕偺岞幃傪曄宍偟偰丄sin丄cos傪巜悢偺宍偵捈偟偰偐傜寁嶼偟傑偡丅夝摎偱偼幃傪偛偪傖偛偪傖偄偠偭偰偐傜僆僀儔乕偺岞幃傪戙擖偟偰傑偡偑丄偄偒側傝sin丄cos偵戙擖偟偰傕栤戣側偄偱偡丅

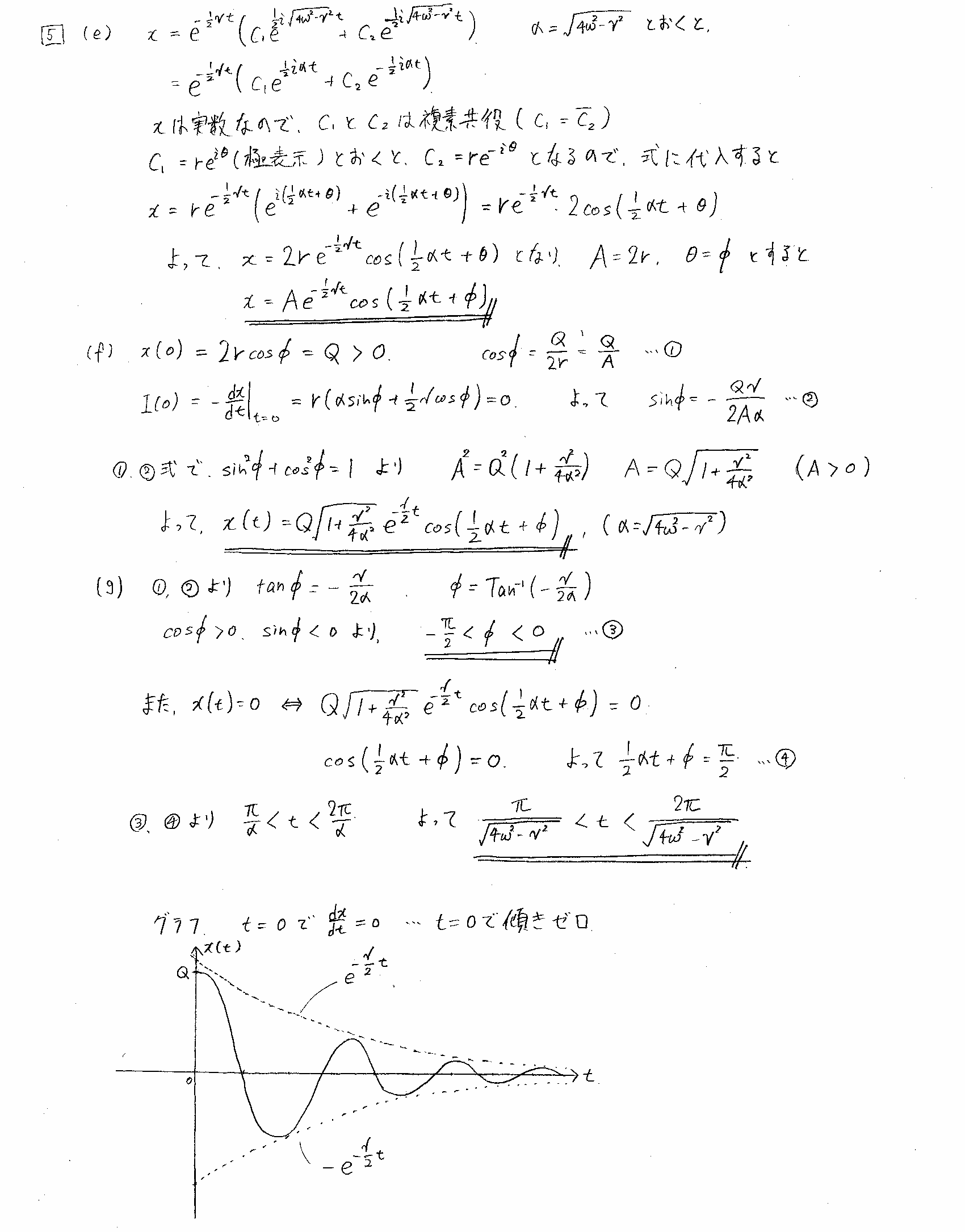
栤5丂揹婥夞楬偲旝暘曽掱幃
丂丂(c)偺旝暘曽掱幃傪夝偔偲偙傠偱偼丄悢棟暔棟妛嘥偱傗偭偰偄傞傛偆偵偲偒傑偡丅(e)偼丄2偮偺掕悢傪re亇i兤偲嬌昞帵偟偰傑偲傔偰偄偒傑偡丅(g)偱丄乽愨懳抣偑嵟傕彫偝偄暘巬傪偲傞乿偲偄偆昞尰偱偡偑丄廃婜娭悢偱偼摨偠抣傪壗夞傕偲傞偙偲偑偱偒傞偺偱弶婜埵憡傕冇亄(廃婜偺惍悢攞)偲偄偆宍偱柍尷偵偲傞偙偲偑偱偒傑偡丅偦偺柍尷偵偁傞拞偐傜傕偭偲傕愨懳抣偑彫偝偄抣傪弶婜埵憡偲偡傞偲偄偆堄枴偵側傝傑偡丅
傑偨丄(e)偱摼偨夝偺宍偼丄尭彮偡傞巜悢娭悢偺崁偲廃婜娭悢偺愊偵側偭偰偄傞偺偱丄怳暆偑巜悢娭悢揑尭彮傪偡傞cos娭悢丄偲偄偆僌儔僼偵側傝傑偡丅(f)偺栤戣暥偵I(0)=0偲偁傞偺偱丄x=0偱偺僌儔僼偺孹偒偼0偱偡丅
墘廗栤戣偺儁乕僕偵栠傞